La Banda de Moebius
Uno de los objetos matemáticos más famosos dentro y fuera de la propia matemática

Una superficie ordinaria tiene dos caras. Esto se aplica a las superficies cerradas como la esfera y el toro, y a las superficies con contornos curvos, como un disco o un toro del que se haya quitado un trozo.
Las dos caras de una superficie tal, podrían pintarse con colores diferentes para distinguirlas. 
Si la superficie es cerrada, los dos colores nunca se juntan. 
Si la superficie tiene límites curvos, los dos colores se encuentran solamente a lo largo de estas curvas. 
Un bicho que se arrastrara sobre tal superficie y tuviera prohibido cruzar las curvas límites, si existen, siempre quedaría en la misma cara. 
A. F. Möbius hizo el sorprendente descubrimiento de que existen superficies con una sola cara. 
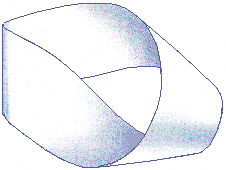
La mas simple de estas superficies es la llamada banda de Möbius, formada tomando una larga tira rectangular de papel y uniendo sus extremos después de darle media vuelta. 
Un bicho que se arrastrara sobre esta superficie, andando siempre por la parte media de la tira, llegaría a su posición original en el lado inferior, como se aprecia en el dibujo del artista gráfico M. C. Escher (1898-1972)

Cualquiera que se comprometiera a pintar una cara de la banda de Möbius podría hacerlo introduciendo toda la tira en un bote de pintura.
Otra propiedad curiosa de la banda de Möbius es que su contorno está formado por una curva simple cerrada. 
La superficie ordinaria de dos lados, formada uniendo los extremos de un rectángulo sin retorcerlo, tiene dos contornos curvos  distintos. 
Si esta última tira se corta a lo largo de la línea central, se rompe en dos tiras distintas de la misma clase. Pero si se corta la banda de Möbius a lo largo de esta línea, encontramos que queda de una sola pieza.
Resulta difícil, para cualquiera que no esté familiarizado con la banda de Möbius, predecir este comportamiento, tan contrario a la intuición de lo que "debería" suceder. 
Si la superficie que resulta de cortar la banda de Möbius a lo largo de su línea media se corta otra vez a lo largo de dicha línea media, se forman dos tiras, separadas pero entrelazadas. 
Es fascinante jugar con tales tiras, cortándolas de parte a parte a lo largo de líneas paralelas al contorno a distancias de 1/2, 1/3, etc. 
Ciertamente, la banda de Möbius merece un lugar en la instrucción geométrica elemental.

Fuente: http://www.fciencias.unam.mx

Aplicaciones

Las bandas de Mobius tienen también utilidad practica. En 1923, Lee Forest obtuvo la patente norteamericana Nº 1.442.632 para una película de esta forma, en la que podrían registrarse ambas caras. Mas recientemente, la misma idea ha sido aplicada a cintas magnetófonicas, con lo que la cinta retorcida puede funcionar el doble de tiempo que lo que estaría otra normal.
Se han otorgado diversas patentes para cintas transportadoras diseñadas a fin de que sufran igual desgaste por ambos lados.
En 1949 O.H. ' obtuvo la patente Nº 2.479.229. relativa a una banda de Mobius abrasiva. B.F. Goodrich se adjudico en 1957 otra patente parecida.
En 1963 J.W. Jacobs consiguió la patente Nº 3.302.795. para un filtro auto limpiante destinado a maquinas de limpieza en seco, que por tener la forma de banda de Mobius facilita el lavado por ambas caras tras sociedad depositada en el filtro al ir este dando vueltas.
Los artistas gráficos se han valido esta banda tanto para fines publicitarios como artísticos. La superficie de Mobius ha tenido también papel destacado en numerosos cuentos de ciencia ficción, No- died Professor, The Wall of darkness. ( julio 1949).
Woldor R.Tobler sugirió en cierta ocasión hacer un mapamundi sobre una superficie de Mobius, de forma que el borde coincidiera con los polos y los paralelos y meridianos quedaran uniformemente separados. De trazarse adecuadamente se podría pinchar el mapa por un punto cualquiera y al asomar la punta por el otro lado señalaria el antípoda esférico.

August Ferdinand Möbius nació en Schulpforta, Alemania, el 17 de noviembre de 1790; fue el único hijo de uno de los más importantes profesores de baile de la aristocracia alemana. Su padre murió cuando él tenía tres años y su madre decidió no mandarlo a la escuela sino hasta que cumplió trece años. En 1803 entró a la escuela de la que salió en 1809 para ingresar a la Universidad de Leipzig. En un principio comenzó estudiando leyes que era la carrera que su familia había decidido para él, pero en menos de un año logró imponer sus gustos a los de su familia y entró a estudiar matemáticas, física y astronomía.
En 1813, Möbius viajó a la ciudad de Göttingen a estudiar bajo la dirección del famosísimo matemático Karl Friedrich Gauss quien en ese entonces era el director del Observatorio de Göttingen. La formación y la pasión por las matemáticas que Möbius recibió de Gauss lo marcaron para toda la vida.
En 1815 fue llamado a formar parte del ejército prusiano y quedó horrorizado. No sólo no quería dejar el estudio de las matemáticas sino que no quería por ningún motivo ingresar a un ejército y participar en una guerra. Finalmente, después de muchos trámites y procesos logró que se le eximiera de ir a la guerra.
En 1816 entró a formar parte del cuerpo de profesores de la universidad de Leipzig y a pesar de que en ese mismo año se le ofreció un puesto como astrónomo en la ciudad de Greifswald y tres años más tarde uno como matemático en Dorpat, nunca abandonó de la universidad de Leipzig.
A partir de entonces se fue convirtiendo en un importante matemático y su nombre quedó ligado a varios objetos matemáticos de distinta especie: la banda de Möbius, la función de Möbius...
Möbius, al igual que la mayoría de los científicos de su época, no se dedicó únicamente a la investigación en matemáticas. Era miembro del observatorio de Leipzig y de hecho fue a él a quién se le encargó su remodelación que duró de 1818 a 1821, para lo cuál visitó varios observatorios de Alemania.
En 1820 se casó y tuvo una hija y dos hijos. En 1848 fue nombrado director del observatorio.

A Möbius le gustaba mucho inventarse problemas y juegos matemáticos:
He aquí uno de ellos:
Un rey con cinco hijos escribió en su testamento que a su muerte sus tierras deberían ser divididas en cinco regiones de tal manera que cada una de las regiones compartiera frontera con las otras cuatro. ¿Tiene solución este problema?
La respuesta es que el problema no tiene solución, sin embargo, es un problema muy intresante que además refleja el profundo interés que Möbius tenía por la topología, área de las matemáticas en la que fue pionero y a la que se dedicó muchos años. Particularmente hizo estudios muy serios sobre las propiedades de las superficies de una sola cara, incluyendo la tan conocida "banda de Möbius" descubierta por él en 1858.
August Möbius murió el 26 de septiembre de 1868 en Leipzig.

Un Curiosidad linguística

Queremos aclarar que quizás en otros lados encontrarás el nombre del matemático Möbius escrito como Moebius, no te preocupes, es exactamente el mismo. Lo que sucede es muchos nombres alemanes llevan "diéresis" (los puntitos que van encima de la o) y antiguamente las máquinas de escribir no tenían este símbolo por lo que en español se optó por escribir las letras "oe" para designar la "ö".
Así por ejemplo, otro gran matemático alemán llamado Gödel muchas veces aparece como Goedel y al famosísimo escritor, también alemán, Göthe, la mayoría de las veces se le encuentra como Goethe.

Fuente: http://redescolar.ilce.edu.mx